建立時間: 2020-09-08 16:34:08

齒形成立的必要條件 (機動學條件)：
Camus 定理
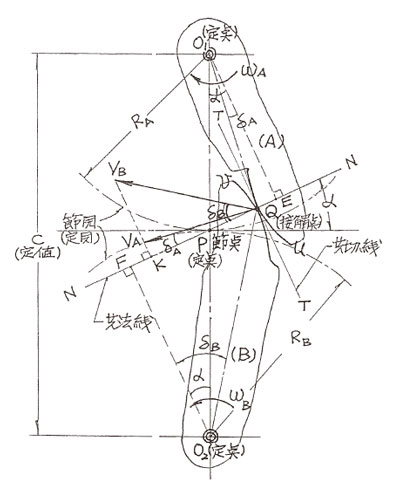
a. 為了要維持一定的轉速比，齒輪齒形在接觸傳動時，其任何時點的共法線必定通過定點 P (節點 )。
b. 齒輪齒形在接觸傳動時，其接觸點 Q 落在節點 P 以外的範圍時，稱其傳動為擦動接觸傳動 (Sliding Contact)。而在接觸傳動其接觸點 Q 正好落在節點 P 上之瞬間時，稱其傳動為純滾動接觸傳動 (Pure Rolling Contact)。
c. 齒輪齒形之接觸傳動，可視為兩個假想節圓，做連續性的純滾動傳動 (Pure Rolling Contact)。
是故，成為齒形曲線會有以下性質：
接觸點 Q 之共法線一定要通過節點 P ( 定點 )，否則無法維持一定的轉速比。
通常運動中的齒輪，其接觸點 Q 不會停留在節點 P 上，只會瞬時經過 P 點，其他時間均在 P 以外的範圍運動。



經過卡謬與歐拉 (李昂哈德 ‧ 歐拉，Leonhard Paul Euler，1707~1783，是一位瑞士數學家和物理學家，近代數學先驅之一，他一生大部分時間在俄國和普魯士度過。歐拉在數學等的多個領域上，包括微積分和圖論都做過重大貢獻。他引進的許多數學術語和書寫格式，例如函數的記法"f(x)"，一直沿用至今。此外，他還在力學、光學和天文學等學科有突出的貢獻 ) 等大師的努力，對擺線齒形的研究已經相當透徹。



不過，此時仍未進入齒輪互換的課題。因定義之故，擺線齒輪中，多齒數齒輪與少齒數齒輪在齒形上是不同的，兩者不具有互換性。

英國劍橋大學教授羅伯特·威利斯牧師 (Robert Willis，1800~1875) 是一位英國語文的學者。他也是第一位獲得廣泛認可的機械工程師的劍橋教授，並且首先在一個令人景仰的基礎上進行元音 (發聲學的母音) 的科學研究。現在威利斯因其廣泛的建築著作(包括關於劍橋大學建築結構的四卷論文) 而廣為人知。

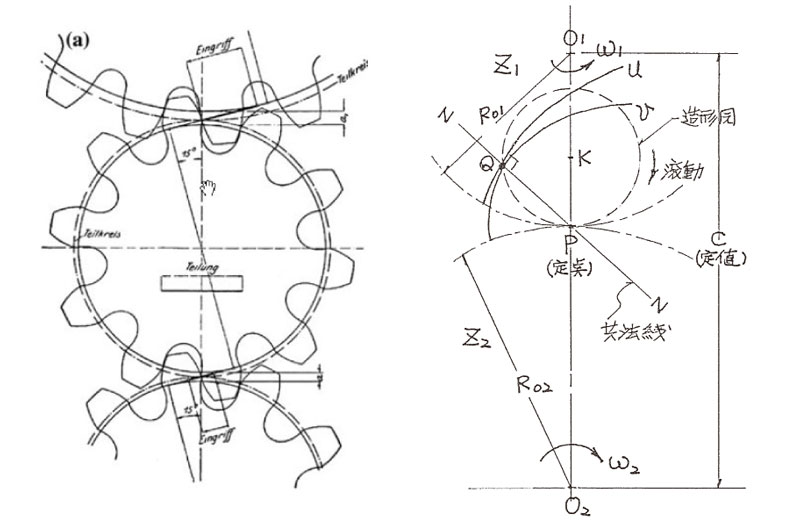
威利斯深入瞭解了卡謬與歐拉對擺現齒形的研究：擺線齒輪是由一個小圓滾一個大圓 (基礎圓，也是節圓 ) 所產生的曲線，若齒數增加，就要換用不同直徑的大圓，所得的曲線自然不同，也難怪不具互換性。當齒數小於 15 齒時，最合適的壓力角為 15 度；而齒形曲線會因為模數、齒數、壓力角，而有所不同。
威利斯因此建議：在相同節距的條件下，對節圓以上的齒形 ( 齒冠部份 ) 採用外擺線，對節圓以下的齒形 ( 齒根部份 ) 採用內擺線，以這樣複合曲線來處理，就可以解決互換性的問題 ( 如下圖 )。



於是，威利斯設計出複合擺線齒形的繪製儀 (Odontograph)，再透過美國 Brown & Sharp 公司工程師 O. J. Beale 著作《Beale's Book on Gear Wheels》與《Practical Treaties on Gearing》兩書，以
及設計出可以製作擺線齒輪樣板銑刀 (Form milling cutter) 的 Odontograph machine 和 Odontengine，至今仍為擺線齒形的設計標準。也由於 Beale，美國 Brown & Sharp，以及 Pratt & Whitney 等公司的努力，使得擺線齒輪具有優勢的地位，甚至壓制並減緩了漸開線齒輪的普及與發展的時程。

在實務上，人們則以數齒為一組，在此範圍內採用相同的齒形，組與組之間則稍予重疊，如此簡化了齒形的複雜度。舉例而言，12~16、16~20、20~24、24~28 各為一組，使用相同齒形。其中，16、20、24 則為兩兩重疊者。齒輪製造完成之後，為達到順利運轉的目標，必須先讓齒輪對相互磨合運轉 (稱為對磨，Lapping) 後才能予以出廠。

也因為各種齒數區間的齒形之不同，製造者與設計者無法以簡馭繁。當時將這種徒然耗費時間的作為，視為理所當然。其實這種現象已經涉及到工業運用上的效率問題，待日後工業需求增加時，勢必成為生產的瓶頸與阻礙。這時就必須另外設法來解決這個現實的課題。

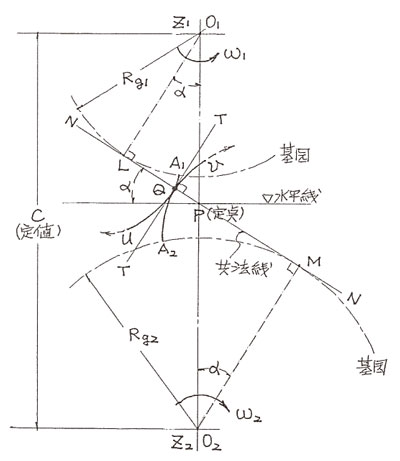
另一方面，由 1765 年瑞士數學家兼物理學歐拉，研究出互相咬合的齒輪，其齒形曲線的曲率半徑和曲率中心位置的關係。由於歐拉尚不知海爾與卡謬的研究成果，遂以獨自的研究途徑在 1754 與 1765 提出了論文。歐拉的研究，其特殊貢獻在於對一組咬合狀態中齒輪齒形曲線之曲率半徑，以及曲率中心的解析，對日後齒形理論提供很大的貢獻。

歐拉曾提出一種齒面是純滾動的齒形，不過卻發現這樣的齒形卻無法達到等速運轉的基本應用要求，亦即運轉不穩定，所以無實用價值。但是形齒面之滾動與擦動關係，即正確齒形之咬合必定是擦動接觸這件事，卻是歐拉最早發現的，這個發現事後更證明漸開線 (Involute) 曲線，也符合了齒形成立的條件(Camus 定理 )。



(下期待續)